Poliedro regular

Um poliedro é considerado regular se for feito de todas as faces idênticas e regulares , e se todos os seus vértices forem idênticos (se houver o mesmo número de arestas que convergem em cada vértice).

Existem cinco poliedros convexos regulares , conhecidos como sólidos platônicos .

Existem quatro poliedros regulares não convexos, conhecidos como sólidos Kepler-Poinsot .

Sólidos platônicos

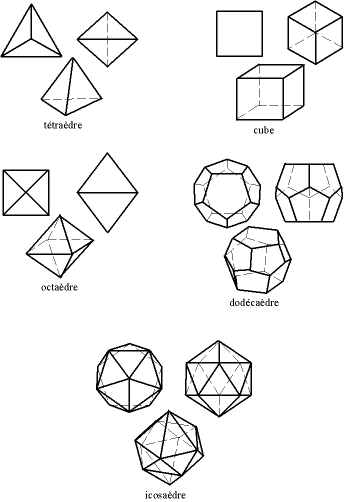
Parece que o próprio Pitágoras (por volta de 530 aC ) ou as Arquitas pitagóricas de Taranto (por volta de 360 aC ) descobriram os três primeiros dos cinco: o tetraedro (a pirâmide), o hexaedro (o cubo), o dodecaedro. Então, Teéteto de Atenas (morreu em 395 ou 369 aC ) descobriu os outros dois: o octaedro e o icosaedro. Platão os usa profundamente em Timeu (54c - 56c), que data de 358 aC. AD Euclides os estuda em seus Elementos (c. 300 aC)

O tetraedro regular (pirâmide)

O tetraedro regular (de tetra , quatro e èdre , base), poliedro com 4 faces triangulares,

consiste em 4 faces em um triângulo equilátero,
tem 4 vértices e 6 arestas.

O hexaedro regular (cubo)

O hexaedro (de hexa , seis e èdre , base)

consiste em 6 faces quadradas,
tem 8 vértices e 12 arestas,
tem 24 triângulos retângulos isósceles .

O octaedro regular

O octaedro (de octa , oito e èdre , base)

consiste em 8 faces em um triângulo equilátero,
tem 6 vértices e 12 arestas,
tem 48 triângulos retângulos escalenos.

O dodecaedro regular

O dodecaedro (de dodecah , doze, e edron , base)

consiste em 12 faces pentagonais iguais,
tem 20 vértices e 30 arestas.

O icosaedro

O icosaedro (de icosa , vinte, e èdre , base)

consiste em 20 faces em um triângulo equilátero ,
tem 12 vértices e 30 arestas,
tem 120 triângulos retângulos escalenos.

Os centros das faces de um sólido platônico são os vértices de um sólido platônico. Essa correspondência é interna entre os tetraedros; ele troca cubos e octaedros de um lado, dodecaedros e icosaedros do outro.

Platão considerava esses sólidos como a imagem da perfeição; para ele, como explica no Timeu , o tetraedro é o símbolo do fogo, o octaedro é o do ar, o icosaedro é o da água, o cubo é da terra e o dodecaedro é o do universo inteiro.

Dois artigos de Cauchy no Journal de l ' École polytechnique tratam de poliedros regulares.

A matemática clássica relaciona esses cinco sólidos regulares à noção de grupo .

Demonstração

Mostraremos que só podem existir os cinco poliedros convexos regulares de Platão; esta demonstração é equivalente à de Euclides.

termos e Condições

Seja $m$ o número de arestas de uma face, $n$ o número de faces que se encontram em um vértice do poliedro ({ m , n } é o símbolo de Schläfli do poliedro). Nós sabemos isso :

$m$ e $n$ são números naturais;
$m \geq 3$ , porque um polígono, que é uma figura bidimensional, tem pelo menos três arestas;
$n \geq 3$ , porque um vértice em um poliedro, figura em três dimensões, não pode unir menos de três faces;
o ângulo de um polígono $m$ regular é igual a graus: 60 graus para um triângulo equilátero, 90 para um quadrado, 108 para um pentágono regular, 120 para um hexágono regular, etc. ; ${\ displaystyle {\ frac {180 (m-2)} {m}}}$
a soma $s$ dos ângulos em um vértice é estritamente inferior a 360 graus, caso contrário, as faces são coplanares ( $s$ = 360 graus) ou sobrepostos ( $s$ > 360 graus).

Equação

Trata-se, portanto, de encontrar todas as soluções do seguinte sistema:

{\ begin {cases} m, n \ in {\ mathbb N} \\ m, n \ geq 3 \\ s (m, n) = {\ frac {180n (m-2)} {m}} <360 \ end {casos}}

Soluções

Se m = 3 (faces triangulares), então os valores adequados são:
- $n = 3$ , porque $s (3,3) = 180 <360$ : é o tetraedro
- $n = 4$ , porque $s (3,4) = 240 <360$ : é o octaedro
- $n = 5$ , porque $s (3,5) = 300 <360$ : é o icosaedro
- Se $n \geq 6$ , o resultado é muito grande: $s (3,6) = 360$ . Na verdade, existem seis triângulos equiláteros com um vértice comum, formando assim um hexágono plano regular.

Se m = 4 (faces quadradas), a única solução é:
- $n = 3$ , porque $s (4,3) = 270 <360$ : é o cubo
- Se $n \geq 4$ , o resultado é muito grande: $s (4,4) = 360$ . Na verdade, existem quatro quadrados com um vértice comum, formando assim um quadrado plano.

Se m = 5 (faces pentagonais):
- $n = 3$ , porque $s (5,3) = 324 <360$ : é o dodecaedro.
- Se $n \geq 4$ , o resultado é muito grande: $s (5,4) = 432> 360$ .

Se $m \geq 6$ , não há mais solução: $s (6,3) = 360$ e se $m \geq 6$ então $s ( m , n ) => 360$ para todo $n \geq 3$ .

Dualidade

Este método também permite identificar poliedros duais , pois basta inverter $m$ e $n$ para obter o dual de um poliedro:

o dual do tetraedro {3,3} é o próprio tetraedro {3,3};
o dual do octaedro {3,4} é o cubo {4.3};
o dual do icosaedro {3,5} é o dodecaedro {5,3}.

Vemos também que o tetraedro é o único autodual, porque, uma vez definido $m = n$ , a única solução completa da equação

s (n, n) = {\ frac {180n (n-2)} {n}} = 180 (n-2) <360

é $n = 3$ , uma vez que $s (3,3) = 180 <360$ ; enquanto com $n = 4$ , o resultado é muito grande: $s (4,4) = 360$ .

Poliedro Kepler-Poinsot

Além dos cinco sólidos platônicos, podemos construir quatro outros sólidos regulares, dois cujas faces são polígonos estrelados regulares (ou cruzados): os sólidos de Kepler , e dois com faces regulares, mas que podem se interpenetrar: os sólidos de Poinsot .

O pequeno dodecaedro estrelado foi descoberto por Kepler vinte e dois séculos depois de Platão, em 1619 . Possui 12 faces que são pentágonos estrela, 12 vértices e 30 arestas. Em cada vértice encontram-se cinco faces. Este pequeno dodecaedro estrela pode ser visto em um mosaico de Paolo Uccello , na Basílica de São Marcos em Veneza , feito aproximadamente em 1430 (quase 200 anos antes de sua descrição matemática).
O grande dodecaedro estelar , descoberto por Kepler, é formado pelos mesmos 12 pentágonos estelares, que possui 20 vértices e também 30 arestas.
O grande dodecaedro descoberto por Poinsot em 1809 . Suas 12 faces são pentágonos regulares, possui 12 vértices e 30 arestas. Mais de 200 anos antes, em sua Perspectiva corporum regularium , um livro em xilogravura publicado em 1568, Wenzel Jamnitzer descreveu o grande dodecaedro.
O grande icosaedro , descoberto por Poinsot, é formado por 20 triângulos equiláteros e que possui 12 vértices e também 30 arestas.

dodecaedro estrelado pequeno {5/2, 5}
grande dodecaedro estrelado {5/2, 3}
grande dodecaedro
{3, 5/2}
grande icosaedro
{5, 5/2}

Notas e referências

Veja também

Link externo

“ Poliedros em movimento ” ( Arquivo • Wikiwix • Archive.is • Google • O que fazer? ) , Em icosaweb.ac-reunion.fr