Quádruplo

Em matemática , uma quádrica , ou superfície quadrática , é uma superfície que satisfaz uma equação cartesiana polinomial de grau 2 com três variáveis (geralmente observadas $x$ , $y$ e $z$ ) da forma

Ax ^ 2 + Por ^ 2 + Cz ^ 2 + 2Dyz + 2Exz + 2Fxy + Gx + Hy + Iz + J = 0

Essas superfícies são classificadas por uma equação reduzida em um sistema de coordenadas ortonormal adaptado na geometria euclidiana , e em nove classes não degeneradas até a transformação linear na geometria afim . Eles também podem ser estudados no âmbito da geometria projetiva , que simplifica e unifica completamente os resultados.

Suas seções planas são cônicas .

A definição é generalizada em dimensão superior com a noção de quádrica afim , uma hipersuperfície , caracterizada como o local de cancelamento (in) de um polinômio de grau 2, mesmo em outro corpo de coeficientes que o dos números reais .

Classificação

Apresentação das principais quádricas

As quádricas não degeneradas são descritas abaixo a partir de suas equações reduzidas em uma estrutura ortonormal adequada.

O elipsóide	$\ frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2} + \ frac {z ^ 2} {c ^ 2} -1 = 0 \,$ ,
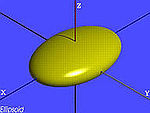
O hiperbolóide de uma folha (H1)	$\ frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2} - \ frac {z ^ 2} {c ^ 2} -1 = 0 \,$ ,
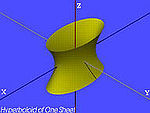
O hiperbolóide de duas folhas (H2)	$\ frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2} - \ frac {z ^ 2} {c ^ 2} +1 = 0 \,$ ,
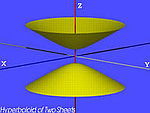
O parabolóide elíptico (PE)	$\ frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2} = z \,$ ,
O parabolóide hiperbólico (PH)	$\ frac {x ^ 2} {a ^ 2} - \ frac {y ^ 2} {b ^ 2} = z \,$ ,
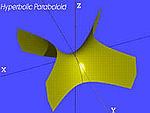
O cone de base elíptico	$\ frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2} - \ frac {z ^ 2} {c ^ 2} = 0 \,$ ,
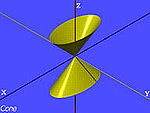
O cilindro elíptico	$\ frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2} -1 = 0 \,$ ,
O cilindro hiperbólico	$\ frac {x ^ 2} {a ^ 2} - \ frac {y ^ 2} {b ^ 2} -1 = 0 \,$ ,
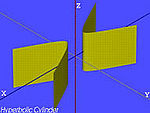
O cilindro parabólico	$\ displaystyle {x ^ 2 = 2 py}$ .

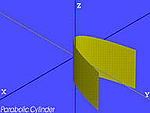
Classificação geral

A equação da superfície pode ser escrita:

Q (x, y, z) + Gx + Hy + Iz + J = 0 ~

onde Q denota a forma quadrática

Q (x, y, z) = Ax ^ 2 + Por ^ 2 + Cz ^ 2 + 2Dyz + 2Exz + 2Fxy ~

matriz:

M_Q = \ begin {pmatrix} A & F & E \\ F & B & D \\ E & D & C \ end {pmatrix}

cujos autovalores são todos reais visto que esta matriz é simétrica real .

A assinatura da forma quadrática é o par (p, q) , onde P é o número de valores próprios positivos estritamente de Q e Q o número de valores próprios estritamente negativos. A classificação de Q é então p + q . Por definição de uma quádrica, a classificação de Q não pode ser zero. O fato de a assinatura de uma forma quadrática não depender da escolha da base escolhida é demonstrado pela lei da inércia de Silvestre .

Quando o posto é igual a 3, a quádrica admite um centro de simetria.

Classificação	Assinatura	Quádrica não degenerada	Quádrica degenerada
3	(3,0) ou (0,3)	elipsóide	$\ varnothing$ ou ponto
3	(2,1) ou (1,2)	hiperbolóide com 1 ou 2 camadas ou cone
2	(2.0) ou (0.2)	parabolóide elíptico ou cilindro elíptico	$\ varnothing$ ou certo
2	(1,1)	cilindro hiperbólico parabolóide ou hiperbólico	encontro de dois planos
1	(1,0) ou (0,1)	cilindro parabólico	$\ varnothing$ ou plano ou combinação de dois planos

Demonstração

Para simplificar, as coordenadas serão sempre anotadas x , y e z , após as várias mudanças de marcas de referência ortonormais que se seguirão.

A matriz da forma quadrática, valores nominais limpas , , , é diagonalizado utilizando uma matriz de transformação ortogonal. Em um novo sistema de coordenadas ortonormal, a equação da superfície é escrita $\ alpha ~$ $\ beta ~$ $\ gamma ~$

\ alpha x ^ 2 + \ beta y ^ 2 + \ gamma z ^ 2 + px + qy + rz = k ~

Quando um dos autovalores não é zero, por exemplo , é possível centralizar a coordenada correspondente: $\ alpha ~$

\ alpha x ^ 2 + px = \ alpha ((x + \ frac {p} {2 \ alpha}) ^ 2 - (\ frac {p} {2 \ alpha}) ^ 2)

que equivale a realizar uma tradução ou mudança de origem do referencial.

Quando a classificação é igual a três, os três valores próprios não são zero; em um novo sistema de coordenadas ortonormal, a equação torna-se:

\ alpha x ^ 2 + \ beta y ^ 2 + \ gamma z ^ 2 = K ~

- se a assinatura vale (3,0) ou (0,3), os três valores próprios têm o mesmo sinal. Se K for zero, é um ponto; caso contrário, é um elipsóide se K tiver o sinal dos autovalores e do conjunto vazio caso contrário.
- se a assinatura vale (2,1) ou (1,2), dois autovalores têm o mesmo sinal, que diremos aqui maioria; se K for zero, é um cone; caso contrário, é um hiperbolóide de uma folha se K tiver o sinal majoritário e um hiperbolóide de duas folhas caso contrário.

Quando a classificação é igual a dois, um dos autovalores é zero e apenas um, por exemplo ; em um novo sistema de coordenadas ortonormal, a equação torna-se: $\ gamma ~$

\ alpha x ^ 2 + \ beta y ^ 2 + rz = K ~

- se r for diferente de zero, obtemos um parabolóide elíptico se os dois autovalores diferentes de zero tiverem o mesmo sinal, e um parabolóide hiperbólico caso contrário, porque a equação está escrita:

\ alpha x ^ 2 + \ beta y ^ 2 = - r (z - \ frac {K} {r}

)

- se r for zero, e se K for zero, é a união de dois planos se os autovalores diferentes de zero forem de sinal oposto e, caso contrário, de linha reta;
- se r for zero e K diferente de zero, é um cilindro hiperbólico se os autovalores diferentes de zero forem de sinal oposto, e se não, de um cilindro elíptico quando K for do sinal dos autovalores diferentes de zero, e l 'vazio definido caso contrário.

Quando a classificação é igual a um, apenas um autovalor é diferente de zero, por exemplo ; em um novo sistema de coordenadas ortonormal, a equação torna-se: $\ beta ~$

\ beta y ^ 2 + px + qy = K ~~

então, após uma última mudança do sistema de coordenadas ortonormal

\ beta y ^ 2 + P x = L ~~

Se P é zero, obtemos um plano se L é zero, e a união de dois planos ou o conjunto vazio, dependendo se L é sinal de ou não. Caso contrário, é um cilindro parabólico. $\beta$

Classificação em geometria afim

Classificação em geometria projetiva

Quádrico em qualquer dimensão

Mais geralmente, em um espaço de dimensão D, se as coordenadas do espaço são , a quádrica geral é uma hipersuperfície definida pela equação algébrica: $\ {x_1, x_2, \ dots, x_D \}$

\ sum_ {i, j = 1} ^ D Q_ {i, j} x_i x_j + \ sum_ {i = 1} ^ D P_i x_i + R = 0

para uma escolha específica de Q, P e R.

A equação normalizada para uma quádrica não degenerada centrada na origem tem a forma:

\ sum_ {i = 1} ^ D \ pm {x_i ^ 2 \ sobre a_i ^ 2} = 1

Formulários

Na modelagem de imagem

Para uma superfície de equação , a fórmula de Taylor-Young fornece uma aproximação local da superfície pela equação quádrica: $z = f (x, y) ~$

p (xa) + q (yb) + \ frac {1} {2} [r (xa) ^ 2 + 2 s (xa) (yb) + t (yb) ^ 2]

com as chamadas notações de Monge $p = \ frac {\ parcial f} {\ parcial x} (a, b), q = \ frac {\ parcial f} {\ parcial y} (a, b), r = \ frac {\ parcial ^ 2 f } {\ parcial x ^ 2} (a, b), t = \ frac {\ parcial ^ 2 f} {\ parcial y ^ 2} (a, b), s = \ frac {\ parcial ^ 2 f} { \ parcial x \ parcial y} (a, b).$

Esta aproximação local é usada na modelagem de imagens, onde fornece resultados interessantes.

Notas e referências

André Warusfel , "Quadriques" , em Dicionário de matemática, álgebra, análise, geometria , Encyclopædia Universalis e Albin Michel,1997.
Nem vazio, nem reduzido a um ponto, a uma reta, a um plano ou à união de dois planos.
Sylvie Philipp, Modelagem Estrutural de Textura. Extração do grão primário e sua regra de colocação no décimo segundo coloque Gretsi , Juan-les-Pins, 1988, Lire en ligne , p. 590 .
Alaa Mustafa, Contribuição ao estudo das curvaturas discretas e suas aplicações , 2008 [Tese].

Veja também

Cônico